用C语言实现dit-fft和dif-fft
|
1,994
|
0
|
C CPP,DSP,大学,编程

843 字
|
26 分钟
关于FFT
实现方法
完整代码

总述：

通过C语言实现先将11位序列进行延拓到1024位后进行fft和ifft变换（要求用dit-fft和dif-fft分别实现）。

一、关于FFT

  • FFT简介：

FFT是一种DFT的高效算法，称为快速傅立叶变换（fast Fourier transform）。傅里叶变换是时域一频域变换分析中最基本的方法之一。在数字处理领域应用的离散傅里叶变换(DFT：Discrete Fourier Transform)是许多数字信号处理方法的基础 。

  • 基本原理：

FFT算法是把长序列的DFT逐次分解为较短序列的DFT。
按照抽取方式的不同可分为DIT-FFT(按时间抽取)和DIF-FFT(按频率抽取)算法。按蝶形运算的构成不同可分为基2，基4，基8，以及任意因子的类型。

  • 迭代关系：

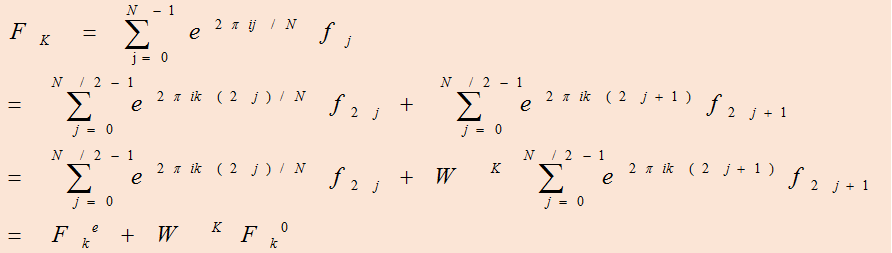
二、实现方法

  • 因为需要进行复数运算，因此定义复数结构体和相关运算
//复数结构体
struct compx
{
    double real;
    double imag;
} compx ;
//两复数相乘
struct compx EE(struct compx b1, struct compx b2)
{
    struct compx b3;
    b3.real = b1.real * b2.real - b1.imag * b2.imag;
    b3.imag = b1.real * b2.imag + b1.imag * b2.real;
    return(b3);
}
//对数计算函数
uint Log(uchar BaseNumber,uint AntiNumber)
{
    uint m=0;
    while(1)
    {
        AntiNumber=AntiNumber/BaseNumber;
        if(AntiNumber)m++;
        else break;
    }
    return m;
}
  • DIT-FFT(按时间抽取)
  1. 进行码位倒置
  2. 再通过蝶形运算
//DIT-FFT函数
void FFT_DIT(struct compx *xin, int N)
{
    int f, m, LH, nm, i, k, j, L;
    double p , ps ;
    int le,B, ip;
    double pi;
    struct compx w, t;
    LH=N / 2;
    f=N;
    for(m = 1;(f = f / 2) != 1; m++){;}    //2的m次方=N，m为级数
    nm = N - 2;
    j = N / 2;
    /*变址运算*/
    for(i = 1;i <= nm; i++)
    {
        if(i < j)
        {
            t = xin[j];
            xin[j] = xin[i];
            xin[i] = t;
        }
        k = LH;
        while(j >= k)
        {
            j = j - k;
            k = k / 2;
        }
        j = j + k;
    }
    /*fft_dit运算*/
    for(L = 0; L <= m - 1; L++)    //每一级
    {
        le =(int) pow(2.0, L + 1);//具有相同旋转因子的蝶形运算的间隔
        B = le / 2; //2的L次方，不同旋转因子的个数，蝶形运算两支间隔
        pi=3.141592653589793;
        for(j = 0;j <= B - 1; j++)
        {
            p = pow(2.0, m - L - 1) * j;
            ps = 2 * pi / N * p;//旋转因子
            w.real = cos(ps);
            w.imag = -sin(ps);
            for(i = j; i <= N - 1; i = i + le)
            {
                ip = i + B;
                t = EE(xin[ip], w);
                xin[ip].real = xin[i].real - t.real;
                xin[ip].imag = xin[i].imag - t.imag;
                xin[i].real = xin[i].real + t.real;
                xin[i].imag = xin[i].imag + t.imag;
            }
        }
    }
    return ;
}
  • DIF-FFT(按频率抽取)
  1. 先进行对应的蝶形运算
  2. 再进行码位倒置
//DIF-FFT函数
void FFT_DIF(struct compx *xin, int N)
{
    int f, m, LH, nm, i, k, j, L;
    double p, ps ;
    int le, B, ip;
    double pi;
    struct compx w, t;
    LH = N / 2;
    f = N;
    for(m = 1; (f = f / 2) != 1; m++){;}//2的m次方=N，m为级数
    /*fft_dif运算*/
    for(L = 0; L <= m - 1; L++)    //每一级
    {
        le =(int) pow(2.0, m - L);//具有相同旋转因子的蝶形运算的间隔
        B = le / 2; //2的m - L - 1次方，不同旋转因子的个数，蝶形运算两支间隔
        pi = 3.141592653589793;
        for(j = 0; j <= B - 1; j++)
        {
            p = pow(2.0, L) * j;
            ps = 2 * pi / N * p;//旋转因子
            w.real = cos(ps);
            w.imag = -sin(ps);
            for(i = j; i <= N-1; i = i + le)
            {
                ip = i + B;
                t = xin[i];
                xin[i].real = t.real + xin[ip].real;
                xin[i].imag = t.imag + xin[ip].imag;
                xin[ip].real = t.real - xin[ip].real;
                xin[ip].imag = t.imag - xin[ip].imag;
                xin[ip] = EE(xin[ip], w);
            }
        }
    }
    nm = N - 2;
    j = N / 2;
    /*变址运算*/
    for(i = 1; i <= nm; i++)
    {
        if(i < j){t = xin[j]; xin[j] = xin[i]; xin[i] = t;}
        k = LH;
        while(j >= k){j = j - k; k = k / 2;}
        j = j + k;
    }
    return ;
}
  • 主程序
int main()
{
    char method,start;	// fft and ifft method
    uint y[12]={1,2,3,4,5,6,7,8,9,0,0}; //输入序列
    int i,j,k;
    FILE *fp;
    fp = fopen("fft_out.txt","w");;
    printf("初始序列:\n");
    fprintf(fp,"初始序列:\n");
    for(i=0;i<94;i++)//长度为MAX的手机号
    {
        for(j=0,k=0;j<11;j++,k=j+i*11)
        {
            if (k == MAX){break;}
            s[k].imag=0;
            s[k].real=y[j];
            printf("%.4f + %.4fi\n",s[k].real,s[k].imag);
            fprintf(fp,"%.4f + %.4fi\n",s[k].real,s[k].imag);
        }
    }
}

三、完整程序代码：

//头文件引用
#include <math.h>
#include <stdio.h>
#include <stdlib.h>


//全局宏定义
#define uint unsigned int
#define uchar unsigned char
#define MAX 1024 //定义序列长度


//复数结构体
struct compx
{
    double real;
    double imag;
} compx ;


//两复数相乘
struct compx EE(struct compx b1, struct compx b2)
{
    struct compx b3;
    b3.real = b1.real * b2.real - b1.imag * b2.imag;
    b3.imag = b1.real * b2.imag + b1.imag * b2.real;
    return(b3);
}


//全局变量定义
uint   Num = 1024;
double result[MAX];
struct  compx s[MAX];
const double pp = 3.141592653589793 ;


//对数计算函数
uint Log(uchar BaseNumber,uint AntiNumber)
{
    uint m=0;
    while(1)
    {
        AntiNumber=AntiNumber/BaseNumber;
        if(AntiNumber)m++;
        else break;
    }
    return m;
}


//DIT-FFT函数
void FFT_DIT(struct compx *xin, int N)
{
    int f, m, LH, nm, i, k, j, L;
    double p , ps ;
    int le,B, ip;
    double pi;
    struct compx w, t;
    LH=N / 2;
    f=N;
    for(m = 1;(f = f / 2) != 1; m++){;}	//2的m次方=N，m为级数
    nm = N - 2;
    j = N / 2;
    /*变址运算*/
    for(i = 1;i <= nm; i++)
    {
        if(i < j)
        {
            t = xin[j];
            xin[j] = xin[i];
            xin[i] = t;
        }
        k = LH;
        while(j >= k)
        {
            j = j - k;
            k = k / 2;
        }
        j = j + k;
    }
    /*fft_dit运算*/
    for(L = 0; L <= m - 1; L++)	//每一级
    {
        le =(int) pow(2.0, L + 1);//具有相同旋转因子的蝶形运算的间隔
        B = le / 2; //2的L次方，不同旋转因子的个数，蝶形运算两支间隔
        pi=3.141592653589793;
        for(j = 0;j <= B - 1; j++)
        {
            p = pow(2.0, m - L - 1) * j;
            ps = 2 * pi / N * p;//旋转因子
            w.real = cos(ps);
            w.imag = -sin(ps);
            for(i = j; i <= N - 1; i = i + le)
            {
                ip = i + B;
                t = EE(xin[ip], w);
                xin[ip].real = xin[i].real - t.real;
                xin[ip].imag = xin[i].imag - t.imag;
                xin[i].real = xin[i].real + t.real;
                xin[i].imag = xin[i].imag + t.imag;
            }
        }
    }
    return ;
}


//DIF-FFT函数
void FFT_DIF(struct compx *xin, int N)
{
    int f, m, LH, nm, i, k, j, L;
    double p, ps ;
    int le, B, ip;
    double pi;
    struct compx w, t;
    LH = N / 2;
    f = N;
    for(m = 1; (f = f / 2) != 1; m++){;}//2的m次方=N，m为级数
    /*fft_dif运算*/
    for(L = 0; L <= m - 1; L++)	//每一级
    {
        le =(int) pow(2.0, m - L);//具有相同旋转因子的蝶形运算的间隔
        B = le / 2; //2的m - L - 1次方，不同旋转因子的个数，蝶形运算两支间隔
        pi = 3.141592653589793;
        for(j = 0; j <= B - 1; j++)
        {
            p = pow(2.0, L) * j;
            ps = 2 * pi / N * p;//旋转因子
            w.real = cos(ps);
            w.imag = -sin(ps);
            for(i = j; i <= N-1; i = i + le)
            {
                ip = i + B;
                t = xin[i];
                xin[i].real = t.real + xin[ip].real;
                xin[i].imag = t.imag + xin[ip].imag;
                xin[ip].real = t.real - xin[ip].real;
                xin[ip].imag = t.imag - xin[ip].imag;
                xin[ip] = EE(xin[ip], w);
            }
        }
    }
    nm = N - 2;
    j = N / 2;
    /*变址运算*/
    for(i = 1; i <= nm; i++)
    {
        if(i < j){t = xin[j]; xin[j] = xin[i]; xin[i] = t;}
        k = LH;
        while(j >= k){j = j - k; k = k / 2;}
        j = j + k;
    }
    return ;
}


//IFFT1函数
void IFFT_DIT(struct compx *xin, int N)
{
    int f, m, LH, nm, i, k, j, L;
    double p, ps ;
    int le, B, ip;
    double pi;
    struct compx w, t;
    LH = N / 2;
    f=N;
    for(m = 1; (f = f / 2) != 1; m++){;}//2的m次方=N，m为级数
    /*fft_dif运算*/
    for(L = 0; L <= m - 1; L++)	//每一级
    {
        le = (int) pow(2.0, m - L);//具有相同旋转因子的蝶形运算的间隔
        B = le / 2; //2的m - L - 1次方，不同旋转因子的个数，蝶形运算两支间隔
        pi=3.141592653589793 ;
        for(j = 0; j <= B-1; j++)
        {
            p = pow(2.0, L) * j;
            ps = -2 * pi / N * p;//旋转因子
            w.real = cos(ps);
            w.imag = -sin(ps);
            for(i = j; i <= N - 1; i = i + le)
            {
                ip = i + B;
                t = xin[i];
                xin[i].real = (t.real + xin[ip].real) * 0.5;
                xin[i].imag = (t.imag + xin[ip].imag) * 0.5;
                xin[ip].real = (t.real - xin[ip].real) * 0.5;
                xin[ip].imag = (t.imag - xin[ip].imag) * 0.5;
                xin[ip] = EE(xin[ip], w);
            }
        }
    }
    nm = N - 2;
    j = N / 2;
    /*变址运算*/
    for(i = 1; i <= nm; i++)
    {
        if(i < j){t = xin[j]; xin[j]=xin[i]; xin[i]=t;}
        k = LH;
        while(j >= k){j = j - k; k = k / 2;}
        j = j + k;
    }
    return ;
}


//IFFT2函数
void IFFT_DIF(struct compx *xin, int N)
{
    int f, m, LH, nm, i, k, j, L;
    double p, ps ;
    int le, B, ip;
    double pi;
    struct compx w, t;
    LH = N / 2;
    f = N;
    for(m = 1; (f = f / 2) != 1; m++){;}//2的m次方=N，m为级数
    nm = N - 2;
    j = N / 2;
    /*变址运算*/
    for(i = 1; i <= nm; i++)
    {
        if(i < j){t = xin[j]; xin[j] = xin[i]; xin[i] = t;}
        k = LH;
        while(j>=k)
        {
            j = j - k;
            k = k / 2;
        }
        j = j + k;
    }
    /*fft_dit运算*/
    for(L = 0; L <=m - 1; L++)	//每一级
    {
        le=(int) pow(2.0, L + 1);//具有相同旋转因子的蝶形运算的间隔
        B = le / 2; //2的L次方，不同旋转因子的个数，蝶形运算两支间隔
        pi=3.141592653589793 ;
        for(j = 0; j <= B - 1; j++)
        {
            p = pow(2.0, m - L - 1) * j;
            ps = -2 * pi / N * p;//旋转因子
            w.real = cos(ps);
            w.imag = -sin(ps);
            for(i = j; i <= N - 1; i = i + le)
            {
                ip = i + B;
                t = EE(xin[ip], w);
                xin[ip].real = (xin[i].real-t.real) * 0.5;
                xin[ip].imag = (xin[i].imag-t.imag) * 0.5;
                xin[i].real = (xin[i].real+t.real) * 0.5;
                xin[i].imag = (xin[i].imag+t.imag) * 0.5;
            }
        }
    }
    return ;
}

//主函数
int main()
{
    char method,start;	// fft and ifft method
    uint y[12]={1,2,3,4,5,6,7,8,9,0,0}; //输入序列
    int i,j,k;
    FILE *fp;
    fp = fopen("fft_out.txt","w");;
    printf("初始序列:\n");
    fprintf(fp,"初始序列:\n");
    for(i=0;i<94;i++)//长度为MAX的手机号
    {
        for(j=0,k=0;j<11;j++,k=j+i*11)
        {
            if (k == MAX)
            {
                break;
            }
            s[k].imag=0;
            s[k].real=y[j];
            printf("%.4f + %.4fi\n",s[k].real,s[k].imag);
            fprintf(fp,"%.4f + %.4fi\n",s[k].real,s[k].imag);
        }
    }
    while(1)
    {
        printf("Input the fft decimation method(T or t for dit, F or f for dif): ");
        method = getchar();
        if (method == 'T' || method == 't')
        {
            FFT_DIT(s, Num);
            printf("\ndit-fft results:\n");
            fprintf(fp,"\ndit-fft results:\n");
            for(i = 0; i  < Num; i++)
            {
                printf("%.4f", s[i].real);
                printf("+j(%.4f)\n", s[i].imag);
                fprintf(fp,"%.4f +j(%.4f)\n",s[i].real,s[i].imag);
            }
            IFFT_DIT(s, Num);
            printf("\nifft0 results:\n");
            fprintf(fp,"\nifft0 results:\n");
            for(i = 0; i < Num; i++)
            {
                if(i % 11 != 0)
                {
                    printf("%.4f", s[i].real);
                    printf("+j(%.4f)\n", s[i].imag);
                    fprintf(fp,"%.4f +j(%.4f)\n",s[i].real,s[i].imag);
                }
                if(i % 11 == 0)
                {
                    printf("%.4f", s[0].real);
                    printf("+j(%.4f)\n", s[0].imag);
                    fprintf(fp,"%.4f +j(%.4f)\n",s[0].real,s[0].imag);
                }
            }
            break;
        }

        else if (method == 'F' || method == 'f')
        {
            FFT_DIF(s, Num);
            printf("\ndif-fft results:\n");
            fprintf(fp,"\ndif-fft results:\n");
            for(i = 0; i  < Num; i++)
            {
                printf("%.4f", s[i].real);
                printf("+j(%.4f)\n", s[i].imag);
                fprintf(fp,"%.4f +j(%.4f)\n",s[i].real,s[i].imag);
            }
            IFFT_DIF(s, Num);
            printf("\nifft1 results:\n");
            fprintf(fp,"\nifft1 results:\n");
            for(i = 0; i < Num; i++)
            {
                if(i % 11 != 0)
                {
                    printf("%.4f", s[i].real);
                    printf("+j(%.4f)\n", s[i].imag);
                    fprintf(fp,"%.4f +j(%.4f)\n",s[i].real,s[i].imag);
                }
                if(i % 11 == 0)
                {
                    printf("%.4f", s[0].real);
                    printf("+j(%.4f)\n", s[0].imag);
                    fprintf(fp,"%.4f +j(%.4f)\n",s[0].real,s[0].imag);
                }
            }
            break;
        }
        else
        {
            printf("INPUT ERROR!\n");
        }
    }
    FFT_DIF(s, Num);
    printf("\nfft results:\n");
    fprintf(fp,"\nfft results:\n");
    for(i = 0; i  < Num; i++)
    {
        printf("%.4f", s[i].real);
        printf("+j(%.4f)\n", s[i].imag);
        fprintf(fp,"%.4f +j(%.4f)\n",s[i].real,s[i].imag);
    }
    IFFT_DIF(s, Num);
    printf("\nifft2 results:\n");
    fprintf(fp,"\nifft2 results:\n");
    for(i = 0; i < Num; i++)
    {
        if(i % 11 != 0)
        {
            printf("%.4f", s[i].real);
            printf("+j(%.4f)\n", s[i].imag);
            fprintf(fp,"%.4f +j(%.4f)\n",s[i].real,s[i].imag);
        }
        if(i % 11 == 0)
        {
            printf("%.4f", s[0].real);
            printf("+j(%.4f)\n", s[0].imag);
            fprintf(fp,"%.4f +j(%.4f)\n",s[0].real,s[0].imag);
        }
    }
    return 0;
}
用C语言实现dit-fft和dif-fft
暂无评论

发送评论 编辑评论 


				

			

						

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
							
													

					

				

			

			
			

				

					
				

			

				

											

							
							
						

																				
					
											
						

	

		
|´・ω・)ノ
ヾ(≧∇≦*)ゝ
(☆ω☆)
（╯‵□′）╯︵┴─┴
￣﹃￣
(/ω＼)
∠( ᐛ 」∠)＿
(๑•̀ㅁ•́ฅ)
→_→
୧(๑•̀⌄•́๑)૭
٩(ˊᗜˋ*)و
(ノ°ο°)ノ
(´இ皿இ｀)
⌇●﹏●⌇
(ฅ´ω`ฅ)
(╯°A°)╯︵○○○
φ(￣∇￣o)
ヾ(´･ ･｀｡)ノ"
( ง ᵒ̌皿ᵒ̌)ง⁼³₌₃
(ó﹏ò｡)
Σ(っ °Д °;)っ
( ,,´･ω･)ﾉ"(´っω･｀｡)
╮(╯▽╰)╭
o(*////▽////*)q
＞﹏＜
( ๑´•ω•) "(ㆆᴗㆆ)
😂
😀
😅
😊
🙂
🙃
😌
😍
😘
😜
😝
😏
😒
🙄
😳
😡
😔
😫
😱
😭
💩
👻
🙌
🖕
👍
👫
👬
👭
🌚
🌝
🙈
💊
😶
🙏
🍦
🍉
😣
Source: github.com/k4yt3x/flowerhd
	

	

		
颜文字
Emoji
小恐龙
花!
	


									

			

			
			
		

	






下一篇